Fluted Barrel Page
Fluted Barrel
Page

POWERFUL TOOL.... This analysis was done with the LS-DYNA Finite Element Code. This software is a very powerful tool for analyzing the dynamic and static loading of structures. It was used here to calculate the barrel's response to the high pressure gas that forces the bullet out of a barrel when it is fired. For the earlier calculations, the breach end of the barrel was fixed in space which treats the barrel as a cantilever beam. A 3D model of the complete rifle was required to better capture the barrel dynamics. There is a vertical plane of symmetry in the model and only motions in the vertical direction are calculated.
OBJECTIVE.... The objective of this study was to gain some insight and understanding of the dynamics of various Fluted Rifle Barrel contours. The calculations simulate the gas pressure as a bullet is fired. The deformations in the barrel are calculated and then a 100 yard projection of the barrel's muzzle is displayed. I chose the 6PPC caliber because it is the most popular caliber of the benchrest community. I have personally never participated in a benchrest match. However, I am interested in rifle accuracy and how to improve accuracy since varmint hunting also requires very accurate rifles.
THE BARREL.... The 6.657 lb baseline 416 Stainless Steel barrel in this model has a breach diameter of 1.5" for 4 inches and then a straight taper to a diameter of 0.8" at a distance of 20". The diameter is 0.8" from there to the end of the barrel at 22". The caliber is 6mm with no rifling modeled. There are six flutes with a land between the flutes at the top and bottom of the barrel. The width of the lands and flutes are 30 degrees. The flute depth 4" from the breach is 0.25" and it tapers to 0.1" at 20" from the breach. For the increased muzzle sizes the root diameter of the flutes remain 1.0" four inches from the breach and 0.6" at 20" from the breach. The full rifle is in a one G gravitational field to simulate earth's gravity. The barrel's chamber is the approximate size of the 6PPC caliber brass. But for the calculation, I did not include the brass case and merely applied the pressure curve to the bolt face, the chamber walls.
THE ACTION.... The action is 1.5 inches in diameter and is 7.2 inches long. The weight of the action is 2 pounds. The bolt is merged into the actions volume. The gas pressure acts on the bolt face. Since there is no separate bolt, there is also no bolt handle.
THE SCOPE AND RINGS.... The scope weighs approximately 25 oz and is aluminum with a 0.1 inch wall thickness. There is a simulated lens in both the eyepiece and the objective to stiffen the otherwise open ends. The scope rings are also aluminum and are bonded to the action and scope.
THE STOCK.... The "clubby" stock has the mechanical properties of wood. The action is "glued in" to the stock and the barrel is completely free floated. The stock is supported at two places, one 2 inch section near the butt and another 2 inch section on the forearm. The complete rifle is allowed free recoil. There is no shooter's shoulder in the model.
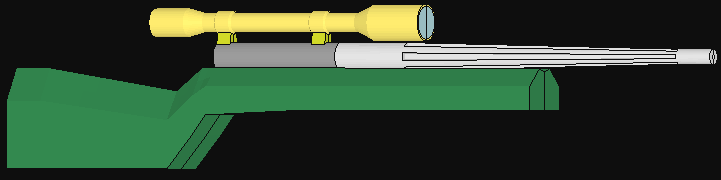
FEA MODEL OF THE RIFLE.... This picture is of the full rifle with the
5.679 lb fluted
barrel and the 0.9" diameter muzzle diameter. The flutes start
4" from the breach and extend to 20" from the breach or 2" from
the muzzle. There are six flutes. The lands and flutes are both 30 degrees wide.
The flutes are positioned for maximum stiffness in the vertical plane with a
land both top and bottom. This puts a flute on each side.
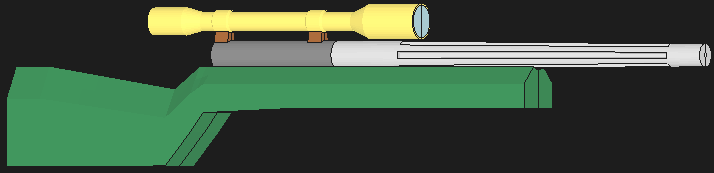
FEA MODEL OF THE RIFLE.... This picture is of the full rifle with the
6.653 lb fluted barrel with a 1.222" diameter muzzle. This barrel weighs the same
as the baseline barrel without fluting. The breach diameter is 1.5" in all
cases.
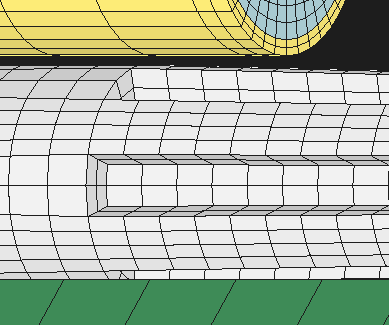
FLUTE CLOSE UP.... This picture shows the flutes at 4" from the
breach. The root diameter of the flutes is 1.0" for all cases. The flutes
root diameter is a straight taper to the muzzle end where it is 0.6" root
diameter. The flutes and lands are each 30 degrees wide. The elements that would
have been a solid barrel were removed for each flute. The ends are square
because that is easiest to model. A real fluted barrel would probably have a tapered lead
out at each end of each flute.
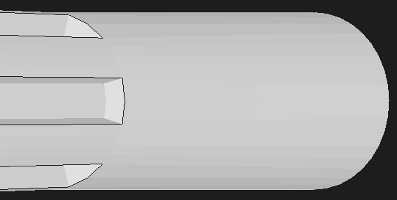
MUZZLE CLOSE UP.... This shows the muzzle of the 0.9" diameter
muzzle and where the flutes end. The root diameter of the flutes is 0.6".
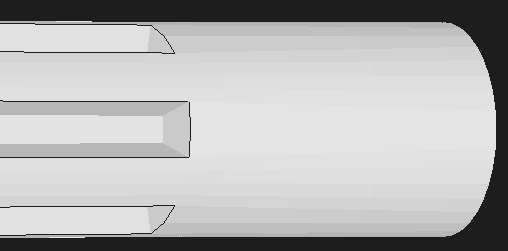
MUZZLE CLOSE UP.... This shows the muzzle of the 1.222" diameter
muzzle and where the flutes end. The root diameter of the flutes is 0.6"
for all cases.
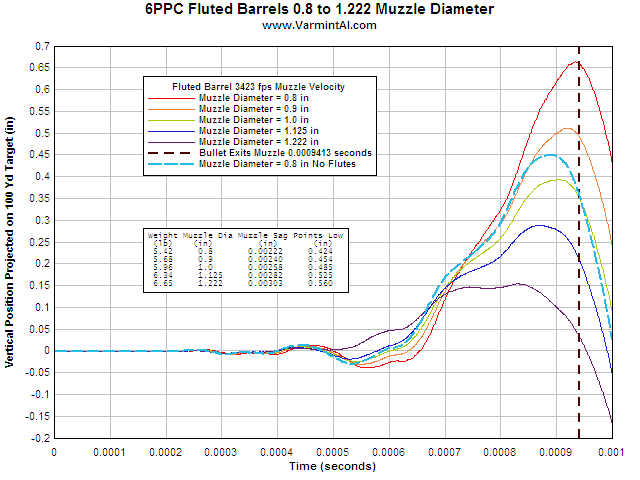
FLUTED BARRELS COMPARED.... This plot shows where the muzzle is pointing
for five different fluted barrels
with muzzle diameters from 0.8" up to 1.222". The muzzle velocity was
3423 fps. I selected the
1.222" inch muzzle diameter barrel because it has the same weight as the
baseline barrel with no flutes. All of the barrels had their muzzles pointing on
a downward swing at bullet exit time. A higher velocity load would possibly time
the bullet exit to the peak of the curve. The pressure curve for Shot 4 was used which
gives a velocity of 3423 fps with a 70 gr bullet exiting the muzzle at 0.0009413
seconds. The curve for the 0.9" muzzle diameter looks very interesting with
the nearly horizontal shape just before bullet exit. I used this 0.9"
muzzle diameter barrel for the five shot comparison with the heavy 1.222"
muzzle diameter barrel.
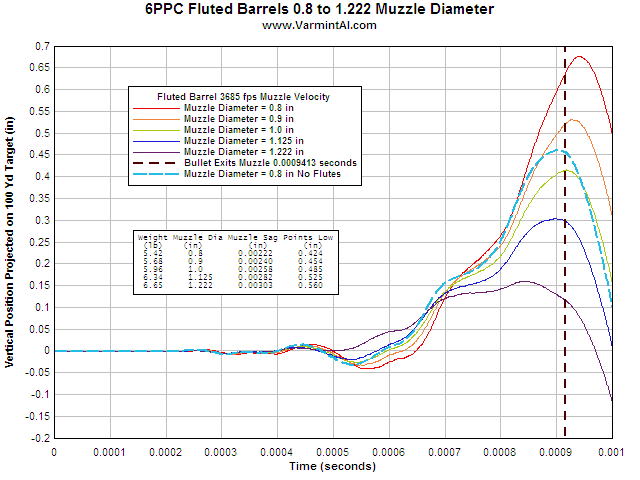
INCREASED MUZZLE VELOCITY.... The same fluted barrels but with a 3685 fps
muzzle velocity. It appears that the first 3 fluted barrels would be pointing to
nearly the same spot on the target for small variations in muzzle velocities
around 3685 fps. But the baseline solid barrel would require even higher
velocities to time the upward pointing swing to bullet exit time. I don't have
pressure vs time data for higher velocity 6PPC loads, but it would be
interesting to calculate the results with higher velocity.
EFFECT OF FLUTING.... Fluting the original barrel reduced its muzzle sag from its own weight by 0.00021 inch. However even with slightly less muzzle sag the fluted barrel will point to a slightly lower place on a 100 yard target by about 0.001 inch.
EFFECT OF EQUAL WEIGHT.... Without changing the breach diameter, fluting a barrel and ending up with the same weight requires a larger muzzle diameter. That process puts more weight near the muzzle assuming there is a non fluted section near the muzzle. The fluted barrel with a 1.222" muzzle diameter has approximately the same weight as the original non fluted barrel but behaves entirely differently in dynamics from the chamber pressure and recoil.
Table A: Fluted Barrel Weights and Deflections
| Number of Flutes |
Muzzle Dia (in) |
Barrel Weight (lb) |
Muzzle Sag (in) |
Points Low at 100 Yd (in) |
| 0 | 0.8 | 6.657 | 0.00243 | 0.4232 |
| 6 | 0.8 | 5.420 | 0.00222 | 0.4242 |
| 6 | 0.9 | 5.679 | 0.00240 | 0.4540 |
| 6 | 1.0 | 5.959 | 0.00258 | 0.4849 |
| 6 | 1.125 | 6.338 | 0.00282 | 0.5254 |
| 6 | 1.222 | 6.653 | 0.00303 | 0.5596 |
![]()
Five Shot Groups
with two Fluted Barrels
 vs
vs 
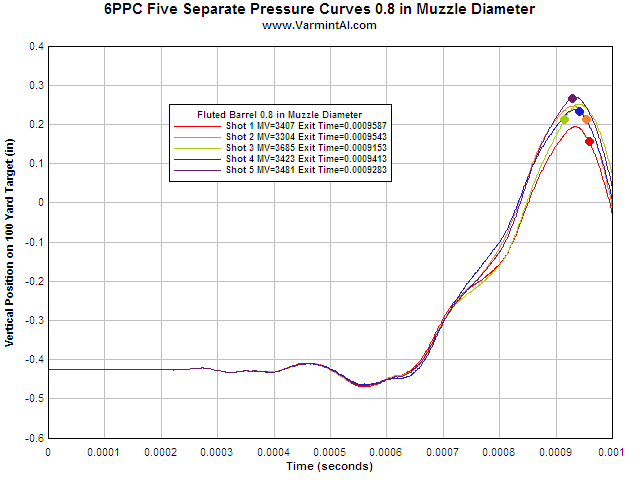

MUZZLE PROJECTION LIGHT FLUTED BARREL.... For the 5.42 lb Fluted Barrel with the
0.8" muzzle, the sag due to gravity causes the muzzle to point
0.3916 inches lower than without including gravity. The muzzle projection is
near a maximum at the bullet exit time for each shot. It appears that the solid
muzzle for 20 inches acts like a tuner in front of the flutes.
![]()
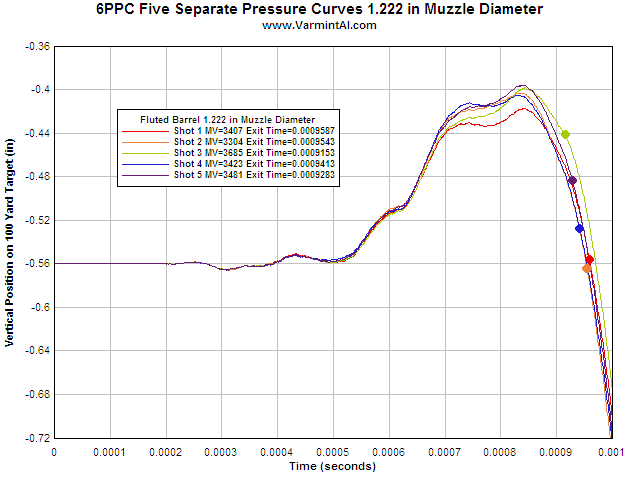

MUZZLE PROJECTION HEAVY FLUTED BARREL.... For the 6.653 lb Heavy Fluted Barrel with the
1.222" muzzle, the sag due to gravity causes the muzzle to point
0.4865" lower than in zero gravity. The rapid swing at
bullet exit time is not good for improved accuracy, but the amplitude is small. It
appears that it would take a large increase of muzzle velocity to put the bullet
exit times near the peak pointing times. The Heavy Fluted Barrel does just about
as well as the Light Fluted Barrel because the downward velocity of the muzzle
is lower than the Light Fluted Barrel.
![]()
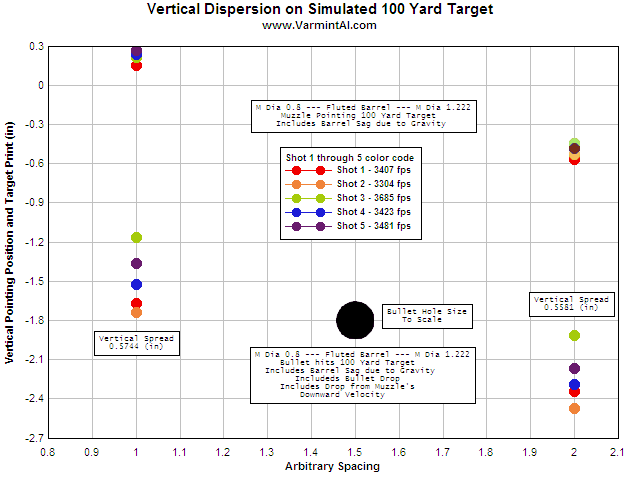
AT THE TARGET.... After all the calculations, here is pictorial summary
and what happens at the virtual 100 yard target. The top "groups" show
where the muzzle is pointing. The bottom "groups" includes the bullet
flight drop, muzzle downward velocity drop and shows where the bullet would hit the target. The vertical plane of symmetry
in the model does not allow for horizontal dispersion. The vertical dispersion
of the two five shot groups is shown in the chart. The highest and lowest
velocity shots increase the group size. There appears to very little improvement
with the heavy fluted barrel. It also appears that fluting is not an accuracy
improvement. The bullet impact points are shown with small colored dots that are
not to scale. The actual size of the bullet holes would have obscured where each
bullet would have hit.
Table 1: Muzzle Projected to a 100 Yard Target
| Shot No. | Muzzle Velocity (fps) |
Bullet Exit Time (seconds) |
Fluted 0.8 MD (inch) |
Fluted 1.222 MD (inch) |
| 1 | 3407 | 0.0009587 | 0.1577 | -0.5554 |
| 2 | 3304 | 0.0009543 | 0.2141 | -0.5634 |
| 3 | 3685 | 0.0009153 | 0.2133 | -0.4412 |
| 4 | 3423 | 0.0009413 | 0.2350 | -0.5274 |
| 5 | 3481 | 0.0009283 | 0.2669 | -0.4827 |
| Maximum Spread Muzzle
Projection Baseline 6.657 lb Barrel = 0.1894 |
0.1092 | 0.1222 | ||
Table 2: Bullet Drop due to the Muzzle's Downward Velocity
at the Time of Bullet Exit
| Shot No. | Muzzle Velocity (fps) |
Bullet Time of Flight (sec) |
Fluted 0.8 MD Muzzle Vertical Velocity (inch/sec) |
Fluted 1.222 MD Muzzle Vertical Velocity (inch/sec) |
Fluted 0.8 MD Downward Velocity Bullet Drop (inch) |
Fluted 1.222 MD Downward Velocity Bullet Drop (inch) |
| 1 | 3407 | 0.093 | -2.741 | -2.298 | -0.255 | -0.214 |
| 2 | 3304 | 0.096 | -2.889 | -2.437 | -0.277 | -0.234 |
| 3 | 3685 | 0.086 | -0.380 | -1.495 | -0.033 | -0.129 |
| 4 | 3423 | 0.092 | -2.123 | -2.164 | -0.196 | -0.200 |
| 5 | 3481 | 0.091 | -1.338 | -1.940 | -0.122 | -0.177 |
Table 3: Muzzle Projected to a 100 Yard Target
Plus the Bullet Drop Calculated from the Muzzle Velocity
| Shot No. | Muzzle Velocity (fps) |
Bullet Drop in 100 Yd (inch) |
Fluted 0.8 MD Including Bullet Drop (inch) |
Fluted 1.222 MD Including Bullet Drop (inch) |
| 1 | 3407 | -1.5724 | -1.6696 | -2.3415 |
| 2 | 3304 | -1.6702 | -1.7334 | -2.4676 |
| 3 | 3685 | -1.3397 | -1.1590 | -1.9095 |
| 4 | 3423 | -1.5569 | -1.5183 | -2.2844 |
| 5 | 3481 | -1.5044 | -1.3593 | -2.1637 |
| Maximum Spread
Including Bullet Drop Baseline 6.657 lb Barrel = 0.7262 |
0.5744 | 0.5581 | ||
ADDING IT ALL TOGETHER.... After including where the muzzle is pointing at the 100 yard target, the bullet drop on it way to the target for each shot's muzzle velocity, and finally the downward velocity of the muzzle swing as the bullet exits, the results show only a slight difference between the 5.420 lb Light Fluted Barrel with the 0.8" muzzle diameter and the 6.653 lb Heavy Fluted Barrel with the 1.222" muzzle diameter. The baseline 6.657 lb non fluted barrel has a maximum spread of 0.7262 with the same five shots. Fluting the baseline barrel showed a reduction in group size of about 21%. Keeping the same weight and fluting the barrel with a 1.222" muzzle diameter reduced the group size by 23%. If fluting is done without introducing large residual stresses in the barrel it should improve accuracy by as much as 20% over a solid barrel of the same contour.


![]()
Earlier Calculations - Practically "Back of the Envelope class"
I have written a small BASIC Program that calculates the stiffness of solid and/or fluted rifle barrels.
I have been reading the postings on the Benchrest Forum about a fluted barrel experiment. It was not clear if the experiment had any value because the fixed end conditions were not specified and the comparison was supposedly to show that cutting flutes in a barrel reduces its stiffness. Any beam loses stiffness when material is removed without changing its length. A much better experiment would have been to use a standard barrel of a given weight and then compare its stiffness to a fluted barrel of the same weight and material. The calculation results below do that. Note: If you find any errors in the calculation, please let me know and I will correct them. My email address is in the table at the left. Thanks.
If one test is worth a thousand opinions, then
one accurate calculation ought to be worth at least 500
opinions!
THE BASIC PROGRAM.... The BASIC program calculates the section moment of inertia for a fluted barrel. (This is not an easy calculation.) In the calculation, there are six flutes with a "land" at the top and bottom of the barrel and a flute on each side of the barrel. The results in the table below are for 22-inch long barrels, except where indicated, with a constant cross section and cantilevered from a rigid wall. The barrel has a 6mm bore. The material in the calculation is 416 stainless steel. I include the barrel OD and its flute dimensions in Table 1. Each flute has a radial edge with a convex arc at its base, which simplifies the calculation. The flutes and lands are of equal width. An actual fluted barrel would have parallel wall flutes and a generous radius at the base of each flute. With these approximations, however one can still observe the affect of fluting on stiffness and barrel end deflection due to gravity (sag).
VARIABLES & UNITS.... I am including the BASIC source program so the viewer can use/improve on it and can critique it for accuracy. As listed, it should run in Quick BASIC. If I can get a friend to port it over to Visual Basic, it will be very easy to use to investigating other barrel configurations. The units are standard English units and are listed in the comment statements. I have each variable defined in the program listing. I will try to make the program more "user friendly" if there is any interest in it. At this point, I have to change the input values and run the program interactively.
|
CONCLUSION ON BARREL FLUTING....
|
FLUTING FOLLY.... Fluting a barrel by cutting circular grooves around the barrel, at intervals along its length, is like putting flexible hinges in the barrel. The stiffness will be greatly reduced. During the Gulf War against Saddam Hussein, Margaret Thatcher allegedly chided the first President Bush 'don't go wobbly, George'. This method of fluting is definitely "wobbly".
Table 1. Results for six different 416 stainless steel 6mm rifle barrels 22" long
| Barrel Weight (lb) |
Barrel OD (in) |
Flute Root Dia (in) |
Flute Depth (in) |
First Mode Natural
Freq (Hz) |
Section Moment of Inertia (in^4) |
Barrel End Sag (in) |
Barrel Exit Angle
Projected to 100 Yard Target (in) |
| 7.222 | 1.250 | none | none | 73.783 | 0.11916 | 0.00278 | 0.6069 |
| 7.222 | 1.3687 | 1.1187 | 0.125 | 75.238 | 0.12390 | 0.00268 | 0.5837 |
| 7.222 | 1.4747 | 0.9747 | 0.250 | 79.278 | 0.13757 | 0.00241 | 0.5257 |
| 7.222 | 1.5674 | 0.8174 | 0.375 | 85.075 | 0.15842 | 0.00209 | 0.4565 |
| 4.820 | 1.2500 | 0.7500 | 0.250 | 67.724 | 0.06700 | 0.00330 | 0.7204 |
| 5.871 | 1.2500 | 1.0000 | 0.125 | 68.619 | 0.08378 | 0.00322 | 0.7017 |
| 4.820* | 1.2500 | none | none | 165.646 | 0.11916 | 0.00052 | 0.1804 |
| 5.871** | 1.2500 | none | none | 111.648 | 0.11916 | 0.00122 | 0.3261 |
* The barrel weight was reduced to 4.820 pounds by shortening the barrel to a length of 14.6829 inches.
** The barrel weight was reduced to 5.871 pounds by shortening the barrel to a length of 17.8845 inches.
BARRELS OF EQUAL WEIGHT.... The results show that a fluted barrel with the same weight as a solid barrel sags less from its own weight. Taking a 1.25 inch diameter cylindrical barrel 22 inches long with a 6mm bore as a standard, it weighs 7.222 pounds. If you make a barrel with the same 7.222 pound weight, but with six 1/4 inch deep flutes, the OD will be 1.4747 inches and the end sag will only be 0.00241 inches, compared to the solid barrel which sags 0.00278 inches. Also, the fluted barrel will vibrate with a higher natural frequency. The end sag is important when considering the vertical jump. As the barrel is pressurized it tends to straighten out like a bourdon tube in a pressure gage. The actual sag is small when compared to the exit angle of the barrel projected to the target. On the standard barrel, the exit angle projected to a 100 yard target would be 0.6069 inches low.
SHORT BARRELS ARE STIFF.... Finally, the overall stiffness of a barrel can be increased by shortening it. The last two examples show a shorter barrel will sag less. The actual section stiffness remains the same, but shortening the barrel removes weight allowing it to sag less. Often, shortening a barrel to reduce its weight is not acceptable for other reasons.
3-D Finite Element Analysis of Four Barrel Configurations
3-D FINITE ELEMENT CALCULATION.... The
Table 2 shows the result of 3-D Finite Element calculations on
four barrels, fluted (0.25 inch deep flutes) and non-fluted. The
first two are straight tapered barrels with a 6mm bore and the
breach end with a 1.25 inch diameter tapered to a muzzle diameter
of 0.900 inch. The material is 416 stainless steel. Each barrel
was configured as a cantilever beam with the left end (breach
end) rigidly fixed and no other support. Only half of the barrel
was modeled and the nodes on the vertical plane were on rollers.
This simplified and greatly reduced the size of the model but
only allows mode shapes that are confined to the vertical plane.
The LS-NIKE3D Finite Element Code, written by John O. Hallquist,
was used for the analysis. Once the calculations were performed
and the output data recorded, the results were post- processed
with the LS-TAURUS Code to display the results.
|
|
|
Table 2. 3-D Finite Element Analysis Results
| Barrel Type all 22 inches long |
Barrel Weight (lb) |
Barrel Sag (in) |
Vibration Mode 1 Frequency (Hz) |
Vibration Mode 2 Frequency (Hz) |
Vibration Mode 3 Frequency (Hz) |
Vibration Mode 4 Frequency (Hz) |
Vibration Mode 5 Frequency (Hz) |
| Solid Taper 1.25-0.9" Dia |
5.299 | 0.00163 | 99.48 | 511.03 | 1337.1 | 2526.4 | 2612.7 |
| Fluted Taper 1.25-0.9" Dia |
4.017 | 0.00134 | 109.15 | 507.96 | 1255.9 | 2367.8 | 2832.2 |
| Full Bull 1.25" Dia No Flutes |
7.223 | 0.00257 | 76.68 | 474.70 | 1304.8 | 2312.5 | 2492.8 |
| Full Bull 1.25" Dia Fluted 6-21" |
5.568 | 0.00181 | 90.71 | 509.66 | 1342.5 | 2430.8 | 2562.4 |
FLUTED BARREL DEFLECTS LESS .... Note that, when cantilevered horizontally, the 4.017 pound fluted barrel with the same OD contour deflects (sags) less than the 5.299 pound solid barrel. The fluted barrel has less stiffness but, even more important, less weight to support. The material removed is from areas that do not efficiently provide support. The reduced weight is better supported by the remaining lands between the flutes. The fluted barrels, in the calculation, were configured such that the flutes started 6 inches from the left end and extended to one inch from the muzzle. The mesh detail is blurred in showing the small mode shape pictures. There is fair agreement between the Finite Element analysis of the Full Bull 1.25 inch diameter barrel 22 inches long and the earlier calculation with the BASIC program. However, the BASIC program only calculated the Mode 1 frequency.
The Table 3 shows the mode shapes for the calculations listed above. They are in the same order as above. The mode shape that is straight is an axial extension/contraction mode. When a round is fired, all of these modes are excited and some energy goes into each vibration mode. The Mode 1 vibration receives most of the energy and the energy is less for each of the succeeding higher frequency modes.

An animated .gif file of the First Mode shape.
Go to the Mode Shape Page to view them
all.
![]() MOVIES OF BARREL MODE SHAPES....
MOVIES OF BARREL MODE SHAPES.... ![]() With the new additional
mirror www.varmintal.net site, I now have room to put the
Mode Shape Page on the web and each movie
can be viewed from the page.
With the new additional
mirror www.varmintal.net site, I now have room to put the
Mode Shape Page on the web and each movie
can be viewed from the page.
Table 3. Mode Shapes in the same order as Table 2.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
The following
is speculation and has not been thoroughly
analyzed.
Note. This was written in 2002.
Since than further analysis has shown this to be the case.
See Esten's Rifle Page for more details.
TIMING.... The approximate time that it takes a 3300 fps muzzle velocity bullet to exit the barrel, assuming a constant acceleration, is 0.0011 seconds. The velocity of sound in 416 stainless steel is 14,900 fps and a stress wave has time to propagate up and back the full length of the barrel 4 or more times after ignition and while the bullet is traveling within the barrel. The muzzle end of the barrel has ample time to "know" that something is going on at the breach end before the bullet exits.
VIBRATION PERIOD.... As an example, assume a mode 1 frequency of approximately 100 Hz that has a period of vibration of 0.010 seconds. Therefore the time it takes the barrel to make its first upward swing is a fourth of a period or about 0.0025 seconds. This is the approximate time the bullet exits. The mode 2 vibration has a period of approximately 0.0002 seconds and could be at the top of its thirteenth upward swing, at the 12.25th period swing, or about 0.0025 seconds. These two modes could add and amplify the exit angle of the muzzle near the peak of its upward swing, just as the bullet exits. The load could be adjusted to slightly change the two frequencies so that they reinforce each other at the time of bullet exit.
FINDING THE SWEET SPOT.... When tuning a load to a
particular rifle, possibly the sweet spot is not when the bullet exits the
barrel at the maximum of the vibration's upward swing but, slightly before the
maximum height or exit angle of the upward swing.
UPWARD SWING.... The vertical amplitude of vibration is more heavily excited than the horizontal
vibration because the center of gravity of the rifle is located below the barrel's
centerline and the bullet's travel down the barrel causes a vertical turning moment
about the rifles center of gravity. The vertical vibration is most important. Also, the
barrel is initially slightly deflected downward due to gravity. When the round is fired, the pressure
also tends to
straighten the barrel like a bourdon tube in a pressure gage. As the barrel
straightens, it over shoots in the upward
direction and this adds to the excitation of the Mode 1 vibration. As a side note,
the axial extension vibration mode is also probably heavily excited. This is the mode where the barrel extends and
shortens axially.
But, this axial mode should only have a negligible affect accuracy.
AVERAGE VELOCITY BULLET.... Possibly the sweet spot occurs when the bullet, with the average velocity, for a
particular load, exits the barrel just before the peak of its upward swing.
FASTER BULLET.... A faster bullet will exit the barrel earlier
and exit slightly before the average velocity bullet and the angle of
the
upward swing of the barrel will be slightly less. So the bullet's
launch angle is slightly less, but the bullet is going faster and drops
less.
SLOWER BULLET.... A slower bullet will exit later and the barrel's vertical swing will be higher
and at a steeper angle when the slower bullet exits. The bullet is launched at a
higher angle but is slower and will drop slightly more.
For a small range of bullet velocities this would tend to print the bullet at about the same vertical location on the target for the normal variations in velocity from round to round.

I have to admit that I like fluted barrels. My Encore in 223 Ackley Improved is
great!
Some Links on Fluting Barrels
Score High Gunsmithing More info on fluting a barrel.
Fulton Armory FAQ More
info on fluting barrels.
Gale McMillan Answer posted on a message board.
Good Hunting... from Varmint Al
For the serious reader: How to Check Another Engineer's Calculation.![]()
Last Updated 07/19/2015
End of Page![]()